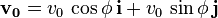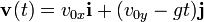Juan londoño.
lunes, 18 de julio de 2011
movimiento en un plano
Plano (geometría)
El plano es un espacio geométrico, que sólo posee dos dimensiones, y contiene infinitos puntos y rectas; es uno de los entes geométricos fundamentales junto con el punto y la recta.
Solamente puede ser definido o descrito en relación a otros elementos geométricos similares. Se suele describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales.
Un plano queda definido por los siguientes elementos geométricos:
- Tres puntos no alineados.
- Una recta y un punto exterior a ella.
- Dos rectas paralelas.
- Dos rectas que se cortan.
Los planos suelen nombrarse con una letra del alfabeto griego.
Suele representarse gráficamente, para su mejor visualización, como una figura delimitada por bordes irregulares (para indicar que el dibujo es una parte de una superficie infinita).
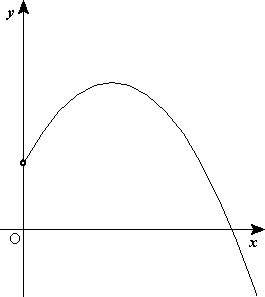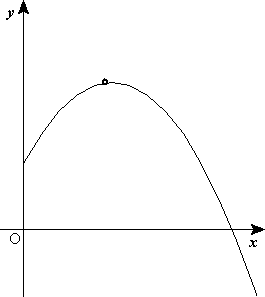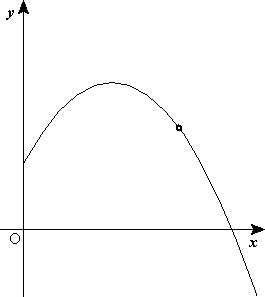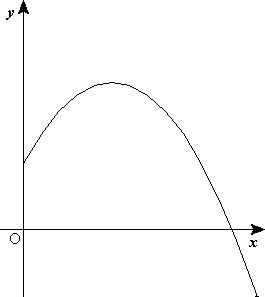
Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico: es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial.  es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal.  es la aceleración de la gravedad.
es la aceleración de la gravedad.
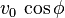 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
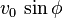 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
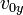
- En lo sucesivo
 : [ecu. 1]
: [ecu. 1]
Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la de la gravedad, que corresponde a la ecuación:Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectória parabólica se puede obtener integrando la siguiente ecuación:La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando la siguiente ecuación diferencial:
Suscribirse a:
Entradas (Atom)